Class notes 9-14 page 21 items 2, 3, 4, 5

Let x = the number of games made at plant 1,
Let y = the number of games made at plant 2.

In the columns of the table, write "times x" next to the numbers in the plant 1 column and write "times y" next to the numbers in the plant 2 column.

The rows of the table give the information needed to write the constraints:  There are only 1700, 1800, and 2400 hours available in the given rows of motherboard production, technical labor, and general manufacturing.
9x + 1y < or = 1700
9x + 3y < or = 1800
4x + 8y < or = 2400
These constraint expressions tell us how much of the resources we can USE.

We want to get as much as we can but we are limited in what we can use.

Graph the constraints using easy points (0,y) and (x,0)

9x + 1y < or = 1700        gives points at ( 0, 1700 ) and ( 188, 0 )

9x + 3y < or = 1800        gives points at ( 0, 600 ) and ( 200, 0 )

4x + 8y < or = 2400        gives points at ( 0, 300 ) and ( 600, 0 )


These lines form a polygonal feasible region.  The vertices (corners) interest us because one of them may give a maximum value for the profit objective function.

The profit objective function is P = 90x + 70y.  This expresses what we want to GET.

In class we estimated that one of the vertices was at (120, 240).  When we plug these quantities of gaming systems into the profit objective function, we get 90(150) + 70(250) = $27,600.

We tried another vertex ( 0, 300 ) in the profit objective function, getting 90(0) + 70(300) = $21,000.

We make more money at the point (120, 240), meaning we should make 120 games at plant 1 and 240 games at plant 2.

Try two other vertices to see if their coordinates give a higher profit.

Math 11 class notes Tuesday September 13

In class we worked through the first part of a system of 3 equations in 3 variables. We used substitution, and we could have used elimination, to make one variable "x" temporarily go away.  We got to 2 equations in two variables, y and z. 

From this point we can again use substitution or elmination to make another variable go away so we can get one equation in one variable to solve..  In real-world problems, systems larger than 3 equations in 3 variables use computers because of the number of calculations involved.  When you learn about matrices, you will be able to use a graphing calculator to more quickly solve such systems.

Homework for Wednesday 9-14, page 21, items 1, 2, 3, 4, 5.  Assign two variables, and write constraints as inequalities.  This assignment is like the one with Roy buying tickets and meals.

From previous classes:

Solving Systems of Equations 9-9

The graphing answer for the bell ringer showed that the two lines crossed in quadrant II.
The slope for the first equation was 2 (uphill) and the slope for the second equation was -4 (downhill)

When we solve a system of two equations in two variables without using graphs, why do we substitute twice?


When we solve a system of two equations in two variables without using graphs, why do we sometimes loof for or try to make terms that cancel each other out (such as 4x and -4x)?


When one of the equations already appears as an isolated "x =" or "y =", what method should you use?


The first part of solving a system of two equations in two variables is to temporarily make one of the variables go away.  You can use the _____________ method or the ____________ method to get one equation in one variable.

The second part of solving the system is to solve for one of the variables.


The third part of solving a system of two equations in two variables is to to bo back through the problem and _________________ what you found for one of the variables so you can bring back the other variable.


Write the solution of an independent and consistent system equations as an ordered pair, such as (-2, 5)


General approach for solving a system:  Make one variable temporarily go away so you have one equation, and solve it.  Use the result to back through the problem, plug it in to bring back the other variable.

Demand and Supply function graphs page 13, item 1, 9-7-2011

The Demand function has a slope of -0.7, so its graph is the one slanted downhill.
The Supply function has a slope of 1.5, so its graph is the one slanted uphill.

Homework for 9-8:  page 14, items 3 and 4, graphing a system of equations.

Vertex Theorem of Linear Programming page 12, item 25, 9-7-2011

Vertex Theorem of Linear Programming

If an ________________________ has a maximum or minimum solution, then that value occurs at one of

the ______________ of the _____________________ .


Increasing the value of the objective function moves its graph in parallel steps away from the origin, as we showed with the yardstick in class  When it reaches the vertex of the feasible region, that gives the maximum values for the x and y that solves the objective function and satisfies the constraints of the feasible region.
.



If an objective function has a maximum or minimum solution, then that value occurs at one of

the vertices (corners) of the feasible region.

Three inequalities form a polygonal region 9-6

Quiz Wednesday, September 6

You will be allowed to use class notes, Cornell notes, blog notes and a calculator.

Not allowed:  Springboard book, printouts from the blog.

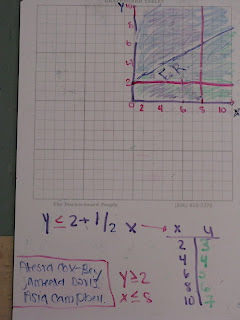
Graph three inequalities and shade the polygonal region.

Describe the effect that introducing constraints has on a region in the coordiante plane.

Given a situation, write an inequality and draw a graph that represents the relationship.

Given a graph, write a linear equation.