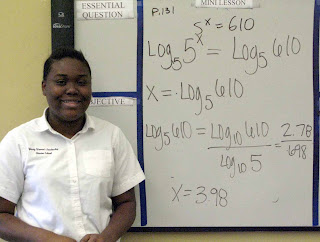Wednesday, December 21, 2011
Friday, December 9, 2011
Prepare for quiz Monday 12-13
Quiz on Monday 12-13. Open notes. Show your work.
Problems will be chosen from p136 items 1, 2, 4 and p137 items 1, 2, 3.
If you were absent or if you have to make up the quiz, alternate problems will be chosen.
Study hints:
Practice using the change of base procedure of dividing the log to the new base of the argument by the log to the new base of the old base.
Practice "de-exponenting" a variable by taking the logarithm in that base. This means using the logarithm and exponent functions as inverses of each other to undo the expression so that the exponent appears without the base.
Practice turning both sides of an equation into exponential expressions using the same base. Do this so you can set the exponents equal to each other.
Practice removing the "log to the base b" symbol from both sides of an equation so you can set the exponents equal to each other.
Know that a base raised to an exponent equals an argument, and that the log to the base of an argument equals an exponent.
Problems will be chosen from p136 items 1, 2, 4 and p137 items 1, 2, 3.
If you were absent or if you have to make up the quiz, alternate problems will be chosen.
Study hints:
Practice using the change of base procedure of dividing the log to the new base of the argument by the log to the new base of the old base.
Practice "de-exponenting" a variable by taking the logarithm in that base. This means using the logarithm and exponent functions as inverses of each other to undo the expression so that the exponent appears without the base.
Practice turning both sides of an equation into exponential expressions using the same base. Do this so you can set the exponents equal to each other.
Practice removing the "log to the base b" symbol from both sides of an equation so you can set the exponents equal to each other.
Know that a base raised to an exponent equals an argument, and that the log to the base of an argument equals an exponent.
Thursday, December 8, 2011
Wednesday, December 7, 2011
12-5 notes - Change of base and graphing calculator
p128, item 20, explain how to evaluate the expression using a graphing calculator.
f(x) = 3 log base 2 (x + 4) - 2
The inside expression is logarithm base 2 of ( x + 4 ). There is no log base 2 key on the calculator, so we need to change the base to 10 so we can use the LOG key.
To change a log expression's base, rewrite the log expression with the new base you want to use.
f(x) = 3 log base 2 (x + 4) - 2
The inside expression is logarithm base 2 of ( x + 4 ). There is no log base 2 key on the calculator, so we need to change the base to 10 so we can use the LOG key.
To change a log expression's base, rewrite the log expression with the new base you want to use.
log base 10 (x + 4)
Divide by the log in the new base of (the number that is the old base)
log base 2 (x + 4) = log base 10 (x + 4)
log base 10 (2)
To finish the problem, use this quotient in a calculator key sequence with the 3 in front and the -2 in back.
y= 3 ( (log (X + 4) divided by log (2)) - 2
enter, trace
Monday, November 28, 2011
11-28 More class notes - Converting to and from logarithmic expressions
If a term uses the log function, and the symbol "log" does not have a subscript, we agree that the base is 10.
The log of a value is the exponent which, when the base 10 is raised to that power, gives the value.
Logarithmic expressions relate a common base, one or more exponents, and one or more values.
To condense a logarithmic expression is to end up with using the log symbol only once.
To expand a logarithmic expression is to start with one use of the log symbol and to end up with several terms using the log symbol.
A non-log expression for a value is turned into a logarithmic expression by using the base of 10 (or deciding on a base), and finding value that makes the statement "10^exponent = value" true.
An expression which multiplies two factors with a common base becomes
a logartihmic expression which adds two exponents.
When you change from a logarithmic expression which adds several log terms to
a non-logarithmic expression, you take out the "log"symbols and use the exponents with
a common base in the factors being multiplied.
The log of a value is the exponent which, when the base 10 is raised to that power, gives the value.
Logarithmic expressions relate a common base, one or more exponents, and one or more values.
To condense a logarithmic expression is to end up with using the log symbol only once.
To expand a logarithmic expression is to start with one use of the log symbol and to end up with several terms using the log symbol.
A non-log expression for a value is turned into a logarithmic expression by using the base of 10 (or deciding on a base), and finding value that makes the statement "10^exponent = value" true.
An expression which multiplies two factors with a common base becomes
a logartihmic expression which adds two exponents.
When you change from a logarithmic expression which adds several log terms to
a non-logarithmic expression, you take out the "log"symbols and use the exponents with
a common base in the factors being multiplied.
11-28 Class notes - Changing expressions from exponential to logarithmic
A relationship with exponents
a^m times a^n = a^(m + n)
implies a relationship between logarithms
log m plus log n = log (m times n)
This is the product rule.
Similarly,
a^m divided by a^n = a^(m - n)
implies
log m minus log n = log (m divided by n)
This is the quotient rule.
a^m times a^n = a^(m + n)
implies a relationship between logarithms
log m plus log n = log (m times n)
This is the product rule.
Similarly,
a^m divided by a^n = a^(m - n)
implies
log m minus log n = log (m divided by n)
This is the quotient rule.
Friday, November 18, 2011
11-18 Class notes - Characteristics of exponential functions
In class we used a graphing calculator to inspect the shapes of growth and decay curves with different bases and initial terms.
In the exponential parent function y = a times b^n . . .
If b is a fraction between zero and 1, the graph shows exponential decay.
If b is greater than 1, the graph shows exponential growth.
If the initial term a is a fraction between zero and 1, the parent graph is compressed vertically, and the slopes at given x's are reduced.
If the initial term a is greater than 1, the parent graph is stretched vertically, and the slopes at given y's are increased.
If the initial term is negative, the parent graph is flipped so that its range falls below the x-axis.
If a constant is added to or subtracted from the parent function, the entire graph is shifted up or down. This is analogous to the value of the y-intercept b in a linear equation altering the height of the line.
In the exponential parent function y = a times b^n . . .
If b is a fraction between zero and 1, the graph shows exponential decay.
If b is greater than 1, the graph shows exponential growth.
If the initial term a is a fraction between zero and 1, the parent graph is compressed vertically, and the slopes at given x's are reduced.
If the initial term a is greater than 1, the parent graph is stretched vertically, and the slopes at given y's are increased.
If the initial term is negative, the parent graph is flipped so that its range falls below the x-axis.
If a constant is added to or subtracted from the parent function, the entire graph is shifted up or down. This is analogous to the value of the y-intercept b in a linear equation altering the height of the line.
Thursday, November 17, 2011
11-17 Class notes Graphs of Exponential Growth and Decay
Use a graphing calculator to enter the sequences
y1= 6 ( 1.2 ) ^ X and
y2= 6 ( 0.9 ) ^ X
TRACE
The y1 graph of an exponential growth curve increases because b, the growth factor, is 1.2 > 1.
The y2 graph of an exponential decay curve decreases because b, the growth factor, is 0.9 < 1.
The general form of an exponential growth function is y = a*b^n where a is the initial value and b is the growth factor, b > 1 and b can not equal 1.
The general form of an exponential decay function is y = a*b^n where a is the initial value and b is the decay factor, b < 1 and b can not equal 1.
The exponent X is how many times we use the growth or decay factor to multiply the initial value.
The domain of the exponential growth and decay functions is x = all real numbers
The range is y > 0.
Homework for 11-22 is page 108, Check Understanding, problems 1, 2, 3.
Shrinking Violets. Hint - the decay factor is 0.8.
y1= 6 ( 1.2 ) ^ X and
y2= 6 ( 0.9 ) ^ X
TRACE
The y1 graph of an exponential growth curve increases because b, the growth factor, is 1.2 > 1.
The y2 graph of an exponential decay curve decreases because b, the growth factor, is 0.9 < 1.
The general form of an exponential growth function is y = a*b^n where a is the initial value and b is the growth factor, b > 1 and b can not equal 1.
The general form of an exponential decay function is y = a*b^n where a is the initial value and b is the decay factor, b < 1 and b can not equal 1.
The exponent X is how many times we use the growth or decay factor to multiply the initial value.
The domain of the exponential growth and decay functions is x = all real numbers
The range is y > 0.
Homework for 11-22 is page 108, Check Understanding, problems 1, 2, 3.
Shrinking Violets. Hint - the decay factor is 0.8.
Wednesday, November 16, 2011
11-16 Class notes Exponential Growth and Decay
Linear functions have the same (constant) slope for any two points on the graph.
A function is non-linear if you can find two pairs of points on the graph with different (non-constant) slopes.
In the table on page 97, the width and length each grew by 20% or .20 with each magnification.
The growth rate is 20% or .20.
To get the new width and length for each successive magnification, you multiply the previous entries by 120% or 1.20.
The growth factor is 120% or 1.20.
The growth factor is the growth rate plus 1
g = r + 1
1.20 = .20 + 1
The growth rate is the growth factor minus 1
r = g - 1
.20 = 1.20 - 1
Negative growth rates are decay rates.
When something grows, the growth factor is greater than 1.
When something decays, the growth factor is less than 1.
In the table on page 99, the y values are halved as x increases by 1. The growth rate is negative 50%, or -.50. We can say that the rate of decay is 50%, or .50.
The decay factor is d = r + 1
.50 = -.50 + 1 This means each successive y is .50 or one-half the previous entry
The decay rate is r = d - 1
-.50 = .50 - 1
Homework for 11-17 is page 100, item 8
A function is non-linear if you can find two pairs of points on the graph with different (non-constant) slopes.
In the table on page 97, the width and length each grew by 20% or .20 with each magnification.
The growth rate is 20% or .20.
To get the new width and length for each successive magnification, you multiply the previous entries by 120% or 1.20.
The growth factor is 120% or 1.20.
The growth factor is the growth rate plus 1
g = r + 1
1.20 = .20 + 1
The growth rate is the growth factor minus 1
r = g - 1
.20 = 1.20 - 1
Negative growth rates are decay rates.
When something grows, the growth factor is greater than 1.
When something decays, the growth factor is less than 1.
In the table on page 99, the y values are halved as x increases by 1. The growth rate is negative 50%, or -.50. We can say that the rate of decay is 50%, or .50.
The decay factor is d = r + 1
.50 = -.50 + 1 This means each successive y is .50 or one-half the previous entry
The decay rate is r = d - 1
-.50 = .50 - 1
Homework for 11-17 is page 100, item 8
Monday, November 14, 2011
11-14 Class notes
Preparation for surprise quiz or open note quiz:
Fill in formulas on page 94, item 16
common ratio of a geometric sequence or series = ____________
the next term divided by the current term
nth term "a sub n" of a geometric series = ____________
the first term times the common ratio r raised to the power n minus 1
partial sum "S sub n" of a geometric series = ____________
the first term times ( 1 minus the common ratio to the nth power / 1 minus the common ratio )
infinite sum "S" of a geometric series = ____________
the first term divided by ( 1 minus the common ratio )
Homework for 10-15 and 10-16: Embedded Assessment 1 The Chessboard Problem
Since the knight takes home all the money on all the squares, we need to think about a series from which we can calculate a partial sum S sub n.
n = 5 or n = 20 or n = 64
In the arithmetic series option, a sub 1 = $1000 = 100000 cents and difference "d" = $1000
Use the formulas for arithmetic series on page 84
common difference of an arithmetic sequence or series = ____________
the next term minus the current term
nth term "a sub n" of an arithmetic series = ____________
the first term plus the common difference d times (n-1)
partial sum "S sub n" of a geometric series = ____________
(the first term a sub 1 plus the last term a sub n) times (n/2)
In the geometric series option, a sub 1 = 1 cent and the ratio "r" = 2
Use the formulas for geometric series on page 94
Fill in formulas on page 94, item 16
common ratio of a geometric sequence or series = ____________
the next term divided by the current term
nth term "a sub n" of a geometric series = ____________
the first term times the common ratio r raised to the power n minus 1
partial sum "S sub n" of a geometric series = ____________
the first term times ( 1 minus the common ratio to the nth power / 1 minus the common ratio )
infinite sum "S" of a geometric series = ____________
the first term divided by ( 1 minus the common ratio )
Homework for 10-15 and 10-16: Embedded Assessment 1 The Chessboard Problem
Since the knight takes home all the money on all the squares, we need to think about a series from which we can calculate a partial sum S sub n.
n = 5 or n = 20 or n = 64
In the arithmetic series option, a sub 1 = $1000 = 100000 cents and difference "d" = $1000
Use the formulas for arithmetic series on page 84
common difference of an arithmetic sequence or series = ____________
the next term minus the current term
nth term "a sub n" of an arithmetic series = ____________
the first term plus the common difference d times (n-1)
partial sum "S sub n" of a geometric series = ____________
(the first term a sub 1 plus the last term a sub n) times (n/2)
In the geometric series option, a sub 1 = 1 cent and the ratio "r" = 2
Use the formulas for geometric series on page 94
Thursday, November 10, 2011
11-10 and 11-14 Matrix quiz additional opportunity
Page 71; items 46a 46b 46c 46d, 47a 47b, 48
I will record the higher of the scores from this assignment and the Matrix quiz from 11-1.
You may use your old quiz, class notes, and the blog.
I will record the higher of the scores from this assignment and the Matrix quiz from 11-1.
You may use your old quiz, class notes, and the blog.
Tuesday, November 8, 2011
11-8 Class notes - Sum of a finite geometric series
Homework for Wednesday 11-9: page 89, items a, b, c.
Hints: "a sub n" is the nth term of a sequence or series.
"a sub 1" is the first term.
"n" is how many terms to include in a partial sum.
"r" is the common ratio that multiplies a term to get the next term.
To find the nth term, use a sub n = a sub 1 times r raised to the n-1 power.
To find the sum up to and including the nth term, use S sub n = a sub 1 times [ (1- r^n) / (1 -r) ]
Don't forget that n is an exponent which raises r to a power. In this formula you don't multiply by n.
If the successive terms are smaller, then r is a fraction or a decimal less than 1. For example, if you take half of the current term to get the next term, the common ratio is 1/2.
An infinite geometric series often approaches a number as the finite sums have more and more terms. This happens when r, the common ratio, is a fraction between -1 and 1.
Hints: "a sub n" is the nth term of a sequence or series.
"a sub 1" is the first term.
"n" is how many terms to include in a partial sum.
"r" is the common ratio that multiplies a term to get the next term.
To find the nth term, use a sub n = a sub 1 times r raised to the n-1 power.
To find the sum up to and including the nth term, use S sub n = a sub 1 times [ (1- r^n) / (1 -r) ]
Don't forget that n is an exponent which raises r to a power. In this formula you don't multiply by n.
If the successive terms are smaller, then r is a fraction or a decimal less than 1. For example, if you take half of the current term to get the next term, the common ratio is 1/2.
An infinite geometric series often approaches a number as the finite sums have more and more terms. This happens when r, the common ratio, is a fraction between -1 and 1.
Friday, November 4, 2011
11-4 Second chance for selected quiz questions
Enough students missed three important problems on Tuesday's matrix quiz that we did similar problems today in order to give partial credit for the missed problems. We multiplied two 2x2 matrices, we found the determinant of a 2x2 matrix, and we found the inverse of a 2x2 matrix.
Students who missed the quiz can make it up after school Monday.
Students who missed the quiz can make it up after school Monday.
Thursday, November 3, 2011
11-3 Class notes Series and sequences
Homework for Friday 11-4: Finish page 83 item 19. Page 84, items 20, 3a, 3b, 3c
Today we began to use summation notation. The part to the right of the Greek letter sigma shows the rule for building the terms of the sequence based on an index, n, that increases. The part with the Greek letter sigma shows the index value for the first term (usually n=1) and the upper limit of n, the number of terms from the beginning of the sequence or series that we want to add up.
"S sub n" and sigma notation identify partial sums of a series, because we could write a series that goes on forever by generating terms of the sequences with n's that go on forever. The sum of an infinite series will be studied next year.
When we convert sigma summation notation into a series of terms, that's called expanding the notation. Sigma notation has a lot of information that we must view as a sequence or as a series in order to apply formulas for nth term, difference, and partial sum (page 84 in your notes).
The vocabulary for sequences and series connects with our everyday speech. If the current term is a sub n, then the previous term is a sub n-1 and the next term is a sub n + 1.
An arithmetic sequence features a common (constant) difference which is used to generate each successive term.
Hint for previous homework page 80, item d.
Use the formula for finding S sub n. Plug in the last term, n, and d and solve for a sub 1 the first term.
To find the nth term when given a first term, a difference, and n, use the formula
a sub n = a sub 1 + (n - 1)*d.
Use subscripts n beneath the letter a to identify which position a value or term has in a series or sequence.
Today we began to use summation notation. The part to the right of the Greek letter sigma shows the rule for building the terms of the sequence based on an index, n, that increases. The part with the Greek letter sigma shows the index value for the first term (usually n=1) and the upper limit of n, the number of terms from the beginning of the sequence or series that we want to add up.
"S sub n" and sigma notation identify partial sums of a series, because we could write a series that goes on forever by generating terms of the sequences with n's that go on forever. The sum of an infinite series will be studied next year.
When we convert sigma summation notation into a series of terms, that's called expanding the notation. Sigma notation has a lot of information that we must view as a sequence or as a series in order to apply formulas for nth term, difference, and partial sum (page 84 in your notes).
The vocabulary for sequences and series connects with our everyday speech. If the current term is a sub n, then the previous term is a sub n-1 and the next term is a sub n + 1.
An arithmetic sequence features a common (constant) difference which is used to generate each successive term.
Hint for previous homework page 80, item d.
Use the formula for finding S sub n. Plug in the last term, n, and d and solve for a sub 1 the first term.
To find the nth term when given a first term, a difference, and n, use the formula
a sub n = a sub 1 + (n - 1)*d.
Use subscripts n beneath the letter a to identify which position a value or term has in a series or sequence.
Friday, October 28, 2011
Preparation for Quiz on Tuesday 11-1
Given a matrix, state its dimensions.
Given two matrices determine whether you can add them, and perform the addition if possible.
Is matrix addition commutative?
Given two matrices determine whether you can multiply them, and perform the multiplication if possible.
Name the method used for matrix multiplication.
Is matrix multiplication commutative?
Write the identity matrix for a given square dimension.
Write the relationship between a matrix A, its inverse, and the identity matrix.
Given a 2x2 square matrix with entries a, b, c, d, find the determinant.
Given a 2x2 square matrix with entries a, b, c, d, find the inverse using the determinant and the rearranged matrix.
Given a system of two equations in two variables, wrtie it in matrix notation with a coefficient matrix, a variable matrix, and a constant matrix.
Given a coefficient matrix, a variable matrix, and a constant matrix, write a corresponding system of linear equations.
Explain how to solve a matrix equation A*X = B.
Multiply a matrix by the identity matrix and show your work.
Given two matrices determine whether you can add them, and perform the addition if possible.
Is matrix addition commutative?
Given two matrices determine whether you can multiply them, and perform the multiplication if possible.
Name the method used for matrix multiplication.
Is matrix multiplication commutative?
Write the identity matrix for a given square dimension.
Write the relationship between a matrix A, its inverse, and the identity matrix.
Given a 2x2 square matrix with entries a, b, c, d, find the determinant.
Given a 2x2 square matrix with entries a, b, c, d, find the inverse using the determinant and the rearranged matrix.
Given a system of two equations in two variables, wrtie it in matrix notation with a coefficient matrix, a variable matrix, and a constant matrix.
Given a coefficient matrix, a variable matrix, and a constant matrix, write a corresponding system of linear equations.
Explain how to solve a matrix equation A*X = B.
Multiply a matrix by the identity matrix and show your work.
Thursday, October 27, 2011
10-27 TI-83 graphing calculator matrix screens
When you first access the MATRIX menu the screen that appears has the names of matrices.
NAMES | MATH | EDIT |
1. The NAMES menu is used to paste the name of a matrix into the home screen or a program.
2. The MATH menu contains all of the operations that can be done with a matrix.
3. The EDIT menu is where you set the size of the menu and enter the elements.
The example below will take you through the basic steps of entering a matrix and using it to solve a system of equations, which is one of the main applications of matrices that you will use in an algebra course.
Example: Use a matrix to solve the following system of equations.
To use a matrix to solve a system of equations, you put the matrix in reduced row echelon form. While this can be a tedious and time consuming process to do by hand, the TI-83 will do this in one step.
Go to MATRIX and EDIT. | |
Define [A] to be a 3X4 matrix. Use the cursor and the ENTER key to move through the spaces. | |
Now enter the coefficients and constants from the system by entering the value and pressing ENTER. | |
Return to the home screen ( the MATRIX MATH menu and scroll down to item B. | |
Hit ENTER to return to the home screen. | |
Enter matrix [A] by pressing and close the parentheses. | |
Press ENTER and read the solution as x=2, y=-1, z=4. |
Matrices can be entered directly into the home screen by using the [ ] keys which are accessed by entering
and

. You enter [ to start the matrix and then enclose each row in [ ] and close the matrix with ]. Below are some screens showing some manipulations with matrices.
Subscribe to:
Comments (Atom)