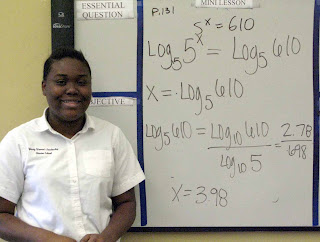Wednesday, December 21, 2011
Friday, December 9, 2011
Prepare for quiz Monday 12-13
Quiz on Monday 12-13. Open notes. Show your work.
Problems will be chosen from p136 items 1, 2, 4 and p137 items 1, 2, 3.
If you were absent or if you have to make up the quiz, alternate problems will be chosen.
Study hints:
Practice using the change of base procedure of dividing the log to the new base of the argument by the log to the new base of the old base.
Practice "de-exponenting" a variable by taking the logarithm in that base. This means using the logarithm and exponent functions as inverses of each other to undo the expression so that the exponent appears without the base.
Practice turning both sides of an equation into exponential expressions using the same base. Do this so you can set the exponents equal to each other.
Practice removing the "log to the base b" symbol from both sides of an equation so you can set the exponents equal to each other.
Know that a base raised to an exponent equals an argument, and that the log to the base of an argument equals an exponent.
Problems will be chosen from p136 items 1, 2, 4 and p137 items 1, 2, 3.
If you were absent or if you have to make up the quiz, alternate problems will be chosen.
Study hints:
Practice using the change of base procedure of dividing the log to the new base of the argument by the log to the new base of the old base.
Practice "de-exponenting" a variable by taking the logarithm in that base. This means using the logarithm and exponent functions as inverses of each other to undo the expression so that the exponent appears without the base.
Practice turning both sides of an equation into exponential expressions using the same base. Do this so you can set the exponents equal to each other.
Practice removing the "log to the base b" symbol from both sides of an equation so you can set the exponents equal to each other.
Know that a base raised to an exponent equals an argument, and that the log to the base of an argument equals an exponent.
Thursday, December 8, 2011
12-9 Student presentations - exponential equations
Cymbrehona Warren solves an exponential equation
Briana Hasan solves an exponential equation
Wednesday, December 7, 2011
12-5 notes - Change of base and graphing calculator
p128, item 20, explain how to evaluate the expression using a graphing calculator.
f(x) = 3 log base 2 (x + 4) - 2
The inside expression is logarithm base 2 of ( x + 4 ). There is no log base 2 key on the calculator, so we need to change the base to 10 so we can use the LOG key.
To change a log expression's base, rewrite the log expression with the new base you want to use.
f(x) = 3 log base 2 (x + 4) - 2
The inside expression is logarithm base 2 of ( x + 4 ). There is no log base 2 key on the calculator, so we need to change the base to 10 so we can use the LOG key.
To change a log expression's base, rewrite the log expression with the new base you want to use.
log base 10 (x + 4)
Divide by the log in the new base of (the number that is the old base)
log base 2 (x + 4) = log base 10 (x + 4)
log base 10 (2)
To finish the problem, use this quotient in a calculator key sequence with the 3 in front and the -2 in back.
y= 3 ( (log (X + 4) divided by log (2)) - 2
enter, trace
12-5 notes - Expand and condense logarithmic expressions
Supports homework p115, p118, p119, p125, p127, and Expand-Condense 2-sided worksheet
Subscribe to:
Posts (Atom)